Daily Maverick
Dailymaverick logo

Maverick News

This article is more than a year old

Maverick News

See the 'unsolvable' problem in the matric maths paper and an expert's possible solution

An alleged error in a trigonometry question in the Grade 12 Mathematics Paper 2 has caused an uproar among learners and teachers. The Department of Basic Education is investigating. While we wait, an expert here explains the problem, and also what it would take to make the question solvable.
See the 'unsolvable' problem in the matric maths paper and an expert's possible solution The 'impossible' seven-mark question in the matric maths exam paper.
Daily Maverick
By Daily Maverick
15 Nov 2022
Facebook
17

The maths problem in question is as follows:

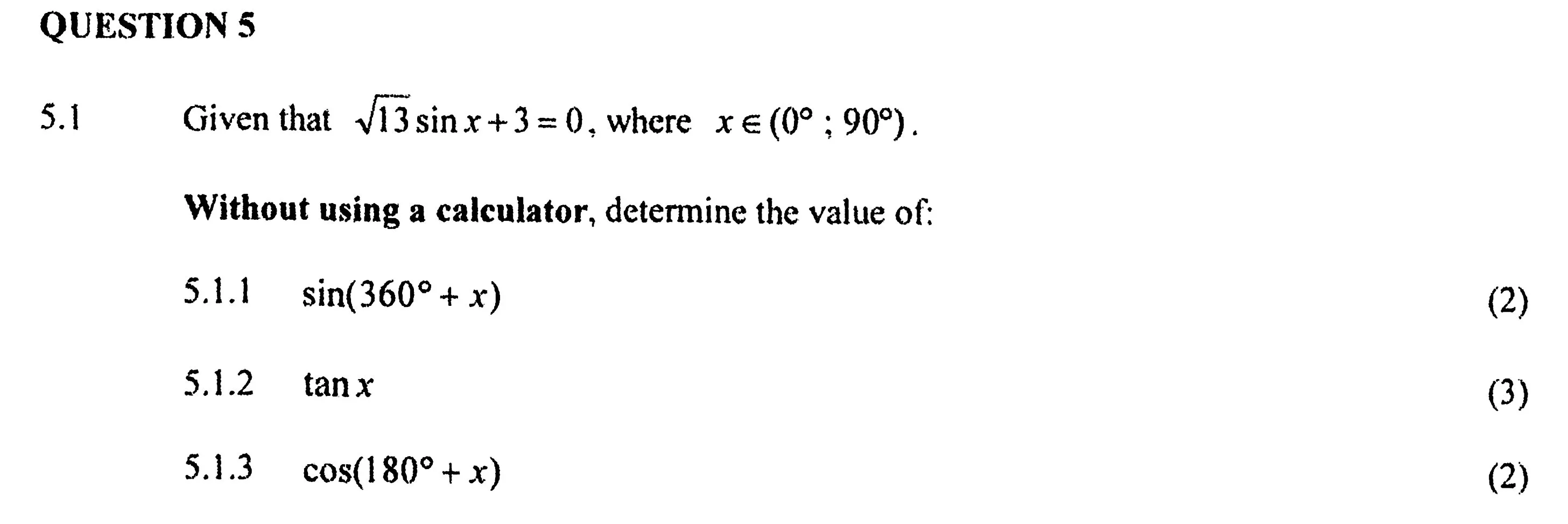trig question The 'impossible' seven-mark question in the matric maths exam paper.



Nicky Roberts, a professor of mathematics education at the University of Fort Hare and director of Kelello Consulting, concluded that the question is impossible to solve. She explained it as follows, and resolved that the only way to solve the problem would be to amend the question.



Read more in Daily Maverick: "Solving the unsolvable 5.1 problem — disastrous matric maths question stumps teachers and learners alike"

[embed]https://www.dailymaverick.co.za/article/2022-01-31-sums-of-all-fears-the-seven-steps-i-used-to-help-my-kids-survive-matric/[/embed]

Comments (5)

Stuart Winckworth Nov 19, 2022, 09:28 AM

Pretty obvious error which any matriculant should pick up immediately. State impossible since sinx for x between ) 0 and 90 is positive and collect full marks for the question so get your 7 marks very quickly and gain time

Andrew Blaine Nov 17, 2022, 07:20 AM

The purpose of an examination is to establish what the examinee knows rather than what they dont. If that is the underlying purpose, how does this question assist the examiner? For 7 marks it seems inappropriate?

Jim Versfeld Nov 16, 2022, 01:42 PM

Prof Roberts is correct - both of the given conditions cannot be true at the same time. The arguments for using the negative square root of 13 are irrelevant, because this number represents the hypotenuse/radius of the circle in which angle x falls, and this value cannot be negative for any angle in the Cartesian Plane. Only the opposite (y-value) and the adjacent (x-value) sides of the triangle can be either negative or positive, depending on which quadrant the angle is in. As stated by Prof Roberts, if the angle is in the first quadrant, the equation can only be solved if +3 is replaced with -3. If the equation is to stand, then the angle must be in the third or fourth quadrant, not in the first as given in the exam paper. I don't think it was meant to be 'diabolical/sneaky/bamboozling/Olympiad-level' at all, probably just sloppy proof-reading. If the proof-reader/external moderator had simply tried to solve the problem, it likely would have been picked up. I think the fairest outcome would be to award full marks for that question to everyone, although that doesn't compensate for the time lost trying to figure it out. Re-writing a whole new whole paper could affect maybe thousands of youngsters who had other commitments.

Chris Crozier Crozier Nov 19, 2022, 08:06 AM

The equation involves a trigonometric function which can be mapped to the properties of a triangle, but just because a constant is in front of the sin(x) that does not make the constant a radius or a hypotenuse. It is just a number multiplying the term. If it had been written as -3.605 sin(x) + 3 = 0 then it would have been solved without great difficulty and with no talk of negative radii (albeit needing a calculator!).

Confucious Says Nov 16, 2022, 09:17 AM

But you only need to be 30% correct!

Glyn Morgan Nov 16, 2022, 08:42 AM

The root of all problems is the ANC. It is always negative.

Easy Does It Nov 16, 2022, 09:55 AM

Agreed 100%. Lets add that the ANC can only add a negative value to any problem or solution. Whether it is square root, root beer, uproot working SOE's a negative vale is expected in an ANC execution of a winning plan.